In der Mathematik ist die Fox H-Funktion
H
(
x
)
{\displaystyle H(x)}
Meijer G-Funktion und der Fox–Wright Funktion , eingeführt von Charles Fox (1961).
Die die Definition ist gegeben durch ein Mellin–Barnes-Integral
H
p
,
q
m
,
n
[
z
|
(
a
1
,
A
1
)
(
a
2
,
A
2
)
…
(
a
p
,
A
p
)
(
b
1
,
B
1
)
(
b
2
,
B
2
)
…
(
b
q
,
B
q
)
]
=
1
2
π
i
∫
L
∏
j
=
1
m
Γ
(
b
j
+
B
j
s
)
∏
j
=
1
n
Γ
(
1
−
a
j
−
A
j
s
)
∏
j
=
m
+
1
q
Γ
(
1
−
b
j
−
B
j
s
)
∏
j
=
n
+
1
p
Γ
(
a
j
+
A
j
s
)
z
−
s
d
s
,
{\displaystyle H_{p,q}^{\,m,n}\!\left[z\left|{\begin{matrix}(a_{1},A_{1})&(a_{2},A_{2})&\ldots &(a_{p},A_{p})\\(b_{1},B_{1})&(b_{2},B_{2})&\ldots &(b_{q},B_{q})\end{matrix}}\right.\right]={\frac {1}{2\pi i}}\int _{L}{\frac {\prod _{j=1}^{m}\Gamma (b_{j}+B_{j}s)\,\prod _{j=1}^{n}\Gamma (1-a_{j}-A_{j}s)}{\prod _{j=m+1}^{q}\Gamma (1-b_{j}-B_{j}s)\,\prod _{j=n+1}^{p}\Gamma (a_{j}+A_{j}s)}}z^{-s}\,ds,}
wobei
L
{\displaystyle L}
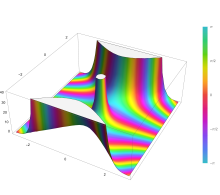
Plot of the Fox H function H((((a 1,α 1),...,(a n,α n)),((a n+1,α n+1),...,(a p,α p)),(((b 1,β 1),...,(b m,β m)),in ((b m+1,β m+1),...,(b q,β q))),z) with H(((),()),(((-1,½)),()),z) Eine Relation der Fox H-Funktion zu den Zweig -1 der Lambertschen W-Funktion ist gegeben durch
W
−
1
(
−
α
⋅
z
)
¯
=
{
lim
β
→
α
−
[
α
2
⋅
(
(
α
−
β
)
⋅
z
)
α
β
β
⋅
H
1
,
2
1
,
1
(
(
α
+
β
β
,
α
β
)
(
0
,
1
)
,
(
−
α
β
,
α
−
β
β
)
∣
−
(
(
α
−
β
)
⋅
z
)
α
β
−
1
)
]
,
falls
|
z
|
<
1
e
|
α
|
lim
β
→
α
−
[
α
2
⋅
(
(
α
−
β
)
⋅
z
)
−
α
β
β
⋅
H
2
,
1
1
,
1
(
(
1
,
1
)
,
(
β
−
α
β
,
α
−
β
β
)
(
−
α
β
,
α
β
)
∣
−
(
(
α
−
β
)
⋅
z
)
1
−
α
β
)
]
,
andernfalls
{\displaystyle {\overline {\operatorname {W} _{-1}\left(-\alpha \cdot z\right)}}={\begin{cases}\lim _{\beta \to \alpha ^{-}}\left[{\frac {\alpha ^{2}\cdot \left(\left(\alpha -\beta \right)\cdot z\right)^{\frac {\alpha }{\beta }}}{\beta }}\cdot \operatorname {H} _{1,\,2}^{1,\,1}\left({\begin{matrix}\left({\frac {\alpha +\beta }{\beta }},\,{\frac {\alpha }{\beta }}\right)\\\left(0,\,1\right),\,\left(-{\frac {\alpha }{\beta }},\,{\frac {\alpha -\beta }{\beta }}\right)\\\end{matrix}}\mid -\left(\left(\alpha -\beta \right)\cdot z\right)^{{\frac {\alpha }{\beta }}-1}\right)\right],\,{\text{falls}}\left|z\right|<{\frac {1}{e\left|\alpha \right|}}\\\lim _{\beta \to \alpha ^{-}}\left[{\frac {\alpha ^{2}\cdot \left(\left(\alpha -\beta \right)\cdot z\right)^{-{\frac {\alpha }{\beta }}}}{\beta }}\cdot \operatorname {H} _{2,\,1}^{1,\,1}\left({\begin{matrix}\left(1,\,1\right),\,\left({\frac {\beta -\alpha }{\beta }},\,{\frac {\alpha -\beta }{\beta }}\right)\\\left(-{\frac {\alpha }{\beta }},\,{\frac {\alpha }{\beta }}\right)\\\end{matrix}}\mid -\left(\left(\alpha -\beta \right)\cdot z\right)^{1-{\frac {\alpha }{\beta }}}\right)\right],\,{\text{andernfalls}}\\\end{cases}}}
wobei
z
¯
{\displaystyle {\overline {z}}}
z
{\displaystyle z}
[1]
Vergleich zur Meijer G-Funktion
G
p
,
q
m
,
n
(
a
1
,
…
,
a
p
b
1
,
…
,
b
q
|
z
)
=
1
2
π
i
∫
L
∏
j
=
1
m
Γ
(
b
j
−
s
)
∏
j
=
1
n
Γ
(
1
−
a
j
+
s
)
∏
j
=
m
+
1
q
Γ
(
1
−
b
j
+
s
)
∏
j
=
n
+
1
p
Γ
(
a
j
−
s
)
z
s
d
s
.
{\displaystyle G_{p,q}^{\,m,n}\!\left(\left.{\begin{matrix}a_{1},\dots ,a_{p}\\b_{1},\dots ,b_{q}\end{matrix}}\;\right|\,z\right)={\frac {1}{2\pi i}}\int _{L}{\frac {\prod _{j=1}^{m}\Gamma (b_{j}-s)\,\prod _{j=1}^{n}\Gamma (1-a_{j}+s)}{\prod _{j=m+1}^{q}\Gamma (1-b_{j}+s)\,\prod _{j=n+1}^{p}\Gamma (a_{j}-s)}}\,z^{s}\,ds.}
Der Spezialfall, für welchen die Fox H-Funktion zur Meijer G-Funktion reduziert wird, ist bei
A
j
=
B
k
=
C
,
C
>
0
{\displaystyle A_{j}=B_{k}=C,C>0}
j
=
1
…
p
{\displaystyle j=1\ldots p}
k
=
1
…
q
{\displaystyle k=1\ldots q}
H
p
,
q
m
,
n
[
z
|
(
a
1
,
C
)
(
a
2
,
C
)
…
(
a
p
,
C
)
(
b
1
,
C
)
(
b
2
,
C
)
…
(
b
q
,
C
)
]
=
1
C
G
p
,
q
m
,
n
(
a
1
,
…
,
a
p
b
1
,
…
,
b
q
|
z
1
/
C
)
.
{\displaystyle H_{p,q}^{\,m,n}\!\left[z\left|{\begin{matrix}(a_{1},C)&(a_{2},C)&\ldots &(a_{p},C)\\(b_{1},C)&(b_{2},C)&\ldots &(b_{q},C)\end{matrix}}\right.\right]={\frac {1}{C}}G_{p,q}^{\,m,n}\!\left(\left.{\begin{matrix}a_{1},\dots ,a_{p}\\b_{1},\dots ,b_{q}\end{matrix}}\;\right|\,z^{1/C}\right).}
Eine Verallgemeinerung der Fox H-Funktion ist geben von Ram Kishore Saxena[2] [3]
↑ Pushpa Narayan and Luan Carlos de Sena Monteiro Rathie and Ozelim: On the Relation between Lambert W-Function and Generalized. Researchgate. Abgerufen am 1. März 2023 (englisch, hypergeometric, functions). ↑ A. M. Mathai, R. K. Saxena: Generalized hypergeometric functions with applications in statistics and physical sciences . Springer, Berlin, New York 1973, ISBN 978-0-387-06482-6 (englisch).
↑ Mathai, A. M.: The H-function with applications in statistics and other disciplines . Wiley, New York 1978, ISBN 978-0-470-26380-8 (englisch).

![{\displaystyle H_{p,q}^{\,m,n}\!\left[z\left|{\begin{matrix}(a_{1},A_{1})&(a_{2},A_{2})&\ldots &(a_{p},A_{p})\\(b_{1},B_{1})&(b_{2},B_{2})&\ldots &(b_{q},B_{q})\end{matrix}}\right.\right]={\frac {1}{2\pi i}}\int _{L}{\frac {\prod _{j=1}^{m}\Gamma (b_{j}+B_{j}s)\,\prod _{j=1}^{n}\Gamma (1-a_{j}-A_{j}s)}{\prod _{j=m+1}^{q}\Gamma (1-b_{j}-B_{j}s)\,\prod _{j=n+1}^{p}\Gamma (a_{j}+A_{j}s)}}z^{-s}\,ds,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1e0af72e03a0f3221f7f5241446802e999ff5b4)

![{\displaystyle {\overline {\operatorname {W} _{-1}\left(-\alpha \cdot z\right)}}={\begin{cases}\lim _{\beta \to \alpha ^{-}}\left[{\frac {\alpha ^{2}\cdot \left(\left(\alpha -\beta \right)\cdot z\right)^{\frac {\alpha }{\beta }}}{\beta }}\cdot \operatorname {H} _{1,\,2}^{1,\,1}\left({\begin{matrix}\left({\frac {\alpha +\beta }{\beta }},\,{\frac {\alpha }{\beta }}\right)\\\left(0,\,1\right),\,\left(-{\frac {\alpha }{\beta }},\,{\frac {\alpha -\beta }{\beta }}\right)\\\end{matrix}}\mid -\left(\left(\alpha -\beta \right)\cdot z\right)^{{\frac {\alpha }{\beta }}-1}\right)\right],\,{\text{falls}}\left|z\right|<{\frac {1}{e\left|\alpha \right|}}\\\lim _{\beta \to \alpha ^{-}}\left[{\frac {\alpha ^{2}\cdot \left(\left(\alpha -\beta \right)\cdot z\right)^{-{\frac {\alpha }{\beta }}}}{\beta }}\cdot \operatorname {H} _{2,\,1}^{1,\,1}\left({\begin{matrix}\left(1,\,1\right),\,\left({\frac {\beta -\alpha }{\beta }},\,{\frac {\alpha -\beta }{\beta }}\right)\\\left(-{\frac {\alpha }{\beta }},\,{\frac {\alpha }{\beta }}\right)\\\end{matrix}}\mid -\left(\left(\alpha -\beta \right)\cdot z\right)^{1-{\frac {\alpha }{\beta }}}\right)\right],\,{\text{andernfalls}}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f1300bcfd5a4d55c52ae6c3c6c849d643f4f8e)






![{\displaystyle H_{p,q}^{\,m,n}\!\left[z\left|{\begin{matrix}(a_{1},C)&(a_{2},C)&\ldots &(a_{p},C)\\(b_{1},C)&(b_{2},C)&\ldots &(b_{q},C)\end{matrix}}\right.\right]={\frac {1}{C}}G_{p,q}^{\,m,n}\!\left(\left.{\begin{matrix}a_{1},\dots ,a_{p}\\b_{1},\dots ,b_{q}\end{matrix}}\;\right|\,z^{1/C}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a258456f0dee32c310e13948bff8e3c8f4bb2de)