Diskussion:Sinus und Kosinus

Diese Diskussionsseite dient dazu, Verbesserungen am Artikel „Sinus und Kosinus“ zu besprechen. Persönliche Betrachtungen zum Thema gehören nicht hierher. Für allgemeine Wissensfragen gibt es die Auskunft.

Füge neue Diskussionsthemen unten an:

Klicke auf Abschnitt hinzufügen, um ein neues Diskussionsthema zu beginnen.

• Diskussionsregeln
• Hilfe zu Diskussionsseiten
• Sei sachlich und freundlich!
• Greife niemanden persönlich an!
• Geh von guten Absichten aus.

Zum Archiv

Automatische Archivierung

Auf dieser Seite werden Abschnitte ab Überschriftenebene 2 automatisch archiviert, die seit 21 Tagen mit dem Baustein {{Erledigt|1=--~~~~}} versehen sind.

angezweifelte Literaturangabe EN 1

Im Juni 2011 wurde eine Literaturangabe (EN 1) angezweifelt. Der Diskussionsbeitrag wurde nie beantwortet. Es wäre gut, wenn jemand mit Zugriff auf die Zeitschrift (z. B. in einer Institutsbibliothek müsste das Periodikum zu finden sein) das nachschauen könnte. Der Diskussionsbeitrag lautete im Original:

Literaturangaben

1J. Ruska, Zur Geschichte des "Sinus". In: Zeitschrift für Mathematik und Physik, Leipzig: Teubner, 1895 : Leider kann ich den Artikel im angegebenen Jahrgang nicht finden; stimmt das Zitat? --888344 12:13, 21. Jun. 2011 (CEST)

Lg --Xeno06 (Diskussion) 23:28, 18. Dez. 2014 (CET)

Siehe hier. Grüße, --Quartl (Diskussion) 16:46, 8. Jan. 2015 (CET)

Super! Ich habe die Onlineverlinkung im EN 1 ergänzt.--Xeno06 (Diskussion) 20:32, 10. Jan. 2015 (CET)

Neues Bild

Hallo zusammen,

ich habe mal wieder ein Bild verbessert:

• 
  Alt
• 
  Neu
• 
  Alternativ

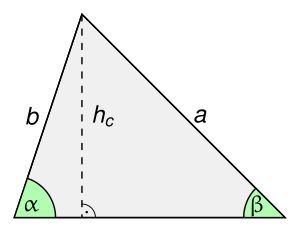
Ich habe den Artikel nicht gelesen und den Abschnitt, in dem das Bild ist nur überflogen. Die Farben scheinen keine Rolle zu spielen. Gibt es Änderungswünsche oder kann man das alte Bild durch mein neues ersetzen?

(@Quartl:, @Digamma: Ihr scheint auch hier mal wieder viel gemacht zu haben. Was sagt ihr?) --Martin Thoma 10:45, 4. Nov. 2015 (CET)

Die Farben spielen keine Rolle, und das neue Bild ist eindeutig besser. --mfb (Diskussion) 17:15, 4. Nov. 2015 (CET)

Für das Beispiel spielen die Farben schon eine Rolle: Im Beispiel werden die rot eingezeichneten Stücke verwendet. Davon abgesehen ist das neue Bild eindeutig besser. --Digamma (Diskussion) 19:43, 5. Nov. 2015 (CET)

Also sollte ich AC und CD rot einfärben, aber das blaue ist nicht nötig? --Martin Thoma 23:48, 5. Nov. 2015 (CET)

Das Beispiel nutzt A, die Höhe und beta, also BC und CD (und beta). AC=b wird nicht verwendet.--mfb (Diskussion) 00:34, 6. Nov. 2015 (CET)

Falls noch etwas an den Farben angepasst wird, bitte darauf achten, dass die Farben rot und grün nicht zusammen in einer Grafik auftauchen, vgl. Rot-Grün-Blindheit.--Christian1985 (Disk) 14:48, 6. Nov. 2015 (CET)

Das ist nur wichtig, wenn das Bild ohne diese Unterscheidung nicht verständlich ist, aber das ist hier nicht der Fall. Außerdem gibt es am Computer sicher Tools, die ggf. bei der Unterscheidung helfen. --mfb (Diskussion) 14:52, 6. Nov. 2015 (CET)

Da habe ich zu oberflächlich gelesen. In diesem Fall machen die bisherigen Farben keinen Sinn. Man kann aber natürlich die Seiten und Winkel austauschen.

Vielleicht sollte man aber das neue Bild auch dazu nutzen, das Beispiel zu erweitern, indem in einem zweiten Schritt aus der Höhe und etwa dem Winkel $\alpha$ die Seite b berechnet wird (oder umgekehrt), im Prinzip also das, was man sonst mit dem Sinussatz tut (und wie man den Sinussatz beweist). Auf verschiedene Farben kann man in diesem Fall verzichten. --Digamma (Diskussion) 17:38, 6. Nov. 2015 (CET)

Hm, ok. Also ich kann gerne etwas mit den Farben anpassen oder auch neue Bilder erstellen, aber mir ist gerade nicht so klar was gewünscht ist.

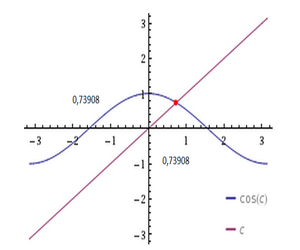
Gerade habe ich noch ein Bild neu gemacht:

• 
  Alt Cos-Fixpunkt
• 
  Neu Cos-Fixpunkt

Viele Grüße, --Martin Thoma 14:59, 7. Nov. 2015 (CET)

Funktionalgleichung

Ich finde den Begriff gestelzt. Meine ganze Ausbildungszeit sowie die entsprechende Literatur begleitete mich mit dem Begriff "Funktionsgleichung".

Ist da ein Unterschied? Wenn ja, welcher? Wenn nicht: bitte Ändern!

Wenn Sie nun argumentieren , dass dies englisch 'functional equiation' heisst, akzeptiere ich das nicht, denn sonst müsste der halbe Duden reformiert werden. --Cosy-ch (Diskussion) 16:42, 17. Jan. 2016 (CET)

Meiner Meinung nach ist „Funktionalgleichung“ der ganz normale und verbreitete Begriff für solche Gleichungen, die eine Funktion bestimmen, siehe auch Funktionalgleichung. Eine „Funktionsgleichung“ ist doch eher so was: $y=f(x)$. Grüße -- HilberTraum (d, m) 17:29, 17. Jan. 2016 (CET)

Das sehe ich auch so! --Christian1985 (Disk) 18:31, 17. Jan. 2016 (CET)

Artikel in anderen Sprachen

Es ist sehr schade, dass lediglich holländisch mit diesem Artikel verlinkt ist. Wie wärs mit anderen wichtigen Sprachen? Je nach Lesart ist Französisch weltweit häufiger benutzt als Deutsch¨! Verlinkung mit Englisch ist ein Muss!

Ein èbertrieben gutes Beispiel ist der französische Wikipedia-Artikel über Cosinus: er ist mit 28 Sprachen verlinkt, bei Deutsch landet man auf dieser Seite!!! --Cosy-ch (Diskussion) 16:45, 17. Jan. 2016 (CET)

Finde ich auch nicht optimal, aber das Problem ist eben, dass fast alle anderen Sprachen getrennte Artikel für Sinus und für Kosinus haben. -- HilberTraum (d, m) 17:34, 17. Jan. 2016 (CET)

Warum handeln wir hier denn zwei Objekte in einem Artikel ab?--Christian1985 (Disk) 18:33, 17. Jan. 2016 (CET)

Die Funktionen sind sich extrem ähnlich. Ist ja nur pi/2 Phasenverschiebung. --mfb (Diskussion) 18:41, 17. Jan. 2016 (CET)

Definition über die Bogenlänge

Die Herleitung über die Parametrisierung des Einheitskreises im Abschnitt 3.4 finde ich hübsch. Gibt es dazu auch ein Buch oder einen Link, wo das so ausgearbeitet ist? --134.76.62.65 20:58, 11. Jun. 2016 (CEST)

Oder so

Korrekte Cosinus-, Sinus- und Tangenswerte berechnen mit 'Plus', 'Minus', 'Mal', 'Geteilt' und mit 'zumQuadrat':

x(1)= -114,588650129332 (entspricht 1°)

x(n+1)=$\textstyle {\frac {x_{1}*(x_{n}^{2}-1)+x_{n}*(x_{1}^{2}-1)}{x_{n}^{2}+x_{1}^{2}+x_{n}*x_{1}}}$

cos(n) = $\textstyle {\frac {2*x_{n}}{x_{n}^{2}-1}}$

sin(n) = $\textstyle {\frac {x_{n}^{2}-1}{x_{n}^{2}+1}}$

tan(n) = $\textstyle {\frac {2*x_{n}}{x_{n}^{2}-1}}$

Probiert's aus, es klappt (Woher x(1) kommt, klären wir wo anders, .. ist auch nicht so schwer)

Gruß, MvBrüsewitz (nicht signierter Beitrag von 79.231.12.142 (Diskussion) 12:16, 28. Jun. 2016 (CEST))

Frage

Wie berechnet man OMA-gerecht aus einem Winkel den Wert des Sinus, ohne andere Winkelfunktionen zu verwenden? Bei 30 Grad und 45 Grad wäre das noch einfach (1/2 und sqrt(2)/2). Danke für die Antwort. -- Karl Bednarik (Diskussion) 04:56, 7. Jul. 2016 (CEST).

Fragen zum Thema bitte auf der Auskunft stellen, die Diskussionsseite dient der Verbesserung der Artikel. Die Reihenentwicklung ist eine Möglichkeit. Moderne Computer haben einige Werte einfach schon gespeichert und interpolieren dann geeignet für einen genaueren Wert. --mfb (Diskussion) 02:39, 10. Jul. 2016 (CEST)

Oder so II

Wenn man meine oben genannte Formel kürzt (Danke HAL),

dann wird aus :

x(n+1)=$\textstyle {\frac {x_{1}*(x_{n}^{2}-1)+x_{n}*(x_{1}^{2}-1)}{x_{n}^{2}+x_{1}^{2}+x_{n}*x_{1}}}$

folgende kürzere Form:

x(n+1)=$\textstyle {\frac {x_{n}*x_{1}-1}{x_{n}+x_{1}}}$

Diese Reihenberechnung erzeugt mit einfachen mathematischen Mitteln

einen nichtlinearen unstet steigeneden Zahlenstrang.

Aus diesem lassen sich die Cosinus-, Sinus-, und Tangenswerte direkt ableiten lassen (s.o.)

cos(n) = $\textstyle {\frac {2*x_{n}}{x_{n}^{2}-1}}$

sin(n) = $\textstyle {\frac {x_{n}^{2}-1}{x_{n}^{2}+1}}$

tan(n) = $\textstyle {\frac {2*x_{n}}{x_{n}^{2}-1}}$

Startwert: x(1) = -114.5886501293 (entspricht 1°)

(x ist hier die Steigung m(s) der Sehne s,

die sich aus sin(w°)/(cos(w°)-1) ergibt.)

Die Formel leitet sich aus dem Additionstheorem ab:

cos(n+1) = cos(n)*cos(1) - sin(n)*sin(1)

sin(n+1) = cos(n)*sin(1) + sin(n)*cos(1)

Sie ist durch Division für die digitale Berechnung "länger",

für's reine Verständnis ist sie aber aber um eine Variable kürzer!

Gruß, MvBruesewitz (nicht signierter Beitrag von 82.73.143.78 (Diskussion) 11:28, 17. Okt. 2016 (CEST))

Eigenartiger Ausdruck unter „Motivation durch Taylorreihen"

Hallo Leute, Ich Habe den Artikel komplett gelesen. 2 Dinge fallen mir eigenartig auf:

1. Den Ausdruck sin^(4n+k)(0) unter dem Abschnitt „Motivation durch Taylorreihen" habe ich noch nie gesehen und es scheint mir unklar was n und k bedeuten sollen.

2. Mir ist trotz Bild unklar wie sich im Abschnitt „Definition am Einheitskreis" tan(α) = sin(α)/cos(α) mithilfe des Strahlensatzes ergibt.

Gruß --2A02:8108:1A00:3000:F49F:2B03:15DB:4CFC 10:45, 23. Nov. 2016 (CET)

reell?

Im Abschnitt Beziehung zur Exponentialfunktion heißt es : "Für eine reelle Zahl {\displaystyle x} x ist also {\displaystyle \cos(x)} {\displaystyle \cos(x)} der Realteil und {\displaystyle \sin(x)} {\displaystyle \sin(x)} der Imaginärteil der komplexen Zahl {\displaystyle \mathrm {e} ^{\mathrm {i} \,x}} \mathrm{e}^{\mathrm{i}\,x}"

sowie kurz darauf: "Diese Gleichung gilt nicht nur für reelle Argumente, sondern für beliebige komplexe Zahlen."

Die beiden Sätze widersprechen einander, mal ist x reell, mal komplex.

Kann das jemand bitte mathematisch fundiert angleichen?

--Fritzbruno (Diskussion) 21:37, 7. Feb. 2017 (CET)

Die Gleichung $\mathrm {e} ^{\mathrm {i} x}=\cos x+\mathrm {i} \cdot \sin x$ gilt immer. Aber nur, wenn x reell ist, sind auch cos x und sin x reell und nur dann ist cos x der Realteil und sin x der Imaginärteil von $\mathrm {e} ^{\mathrm {i} x}$. Es besteht hier also kein Widerspruch. --Digamma (Diskussion) 22:08, 7. Feb. 2017 (CET)

dass die Gleichung immer gilt mag sein, allerdings geht das aus dem Artikel nicht hervor, daher meine Bitte zur Überarbeitung. --Fritzbruno (Diskussion) 23:31, 7. Feb. 2017 (CET)

Im Artikel steht:

Die trigonometrischen Funktionen sind eng mit der Exponentialfunktion verbunden, wie folgende Rechnung zeigt:

${\begin{aligned}\mathrm {e} ^{\mathrm {i} x}&=\sum _{k=0}^{\infty }{\frac {(\mathrm {i} x)^{k}}{k!}}=\sum _{l=0}^{\infty }{\frac {(\mathrm {i} x)^{2l}}{(2l)!}}+\sum _{l=0}^{\infty }{\frac {(\mathrm {i} x)^{2l+1}}{(2l+1)!}}\\&=\underbrace {\sum _{l=0}^{\infty }(-1)^{l}{\frac {x^{2l}}{(2l)!}}} _{\cos x}+\mathrm {i} \underbrace {\sum _{l=0}^{\infty }(-1)^{l}{\frac {x^{2l+1}}{(2l+1)!}}} _{\sin x}\\&=\cos x+\mathrm {i} \sin x\end{aligned}}$

Dabei wurde verwendet $\mathrm {i} ^{2l}=(\mathrm {i} ^{2})^{l}=(-1)^{l}\,$ sowie $\mathrm {i} ^{2l+1}=\mathrm {i} \cdot \mathrm {i} ^{2l}=\mathrm {i} (-1)^{l}$
Somit ergibt sich die sogenannte Eulerformel

$\mathrm {e} ^{\mathrm {i} x}=\cos x+\mathrm {i} \cdot \sin x$.

Hier steht nichts von "reell", somit gilt diese Gleichung für alle x. Von reellen Zahlen ist erst im nächsten Satz die Rede:

Für eine reelle Zahl $x$ ist also $\cos(x)$ der Realteil und $\sin(x)$ der Imaginärteil der komplexen Zahl $\mathrm {e} ^{\mathrm {i} \,x}$.

M.E. ist damit klar, dass die Eulerformel immer gilt, der folgende Satz aber nur für reelle x. Wenn du denkst, dass man das deutlicher machen müsste: Vielleicht kannst du einen Formulierungsvorschlag machen. --Digamma (Diskussion) 18:47, 8. Feb. 2017 (CET)

Eventuell verwirrt hier die verbreitete „Tradition“ reelle Funktionsargumente $x$ zu nennen, komplexe aber $z$. Man könnte vielleicht „vertrauter“ aussehende Formeln haben, indem man $z$ verwendet, wenn explizit der komplexe Fall mit eingeschlossen sein soll? -- HilberTraum (d, m) 20:01, 8. Feb. 2017 (CET)

Formulierung verbessern

Am Ende des Abschnitts 2.2 steht "Hier entspricht dem der Winkel $360^{\circ }$ der Bogenlänge $2\cdot \pi$:" Der Satz ergibt keinen Sinn, jedenfalls keine, den ich verstehe. Könnte jemand mit Fachkenntnis das umformulieren? Danke. --Kartenhörnchen (Diskussion) 13:13, 7. Apr. 2017 (CEST)

Ich hab's geändert:

"Der Winkel wird als Bogenlänge gemessen. Ein Winkel von $360^{\circ }$ entspricht hier einer Bogenlänge von $2\cdot \pi$."

Besser? Gruß--Udo (Diskussion) 13:20, 7. Apr. 2017 (CEST)

Die richtige Bezeichung ist "im Bogenmaß". Habe es geändert. --Digamma (Diskussion) 09:54, 8. Apr. 2017 (CEST)

Warum den Link auf eine WL? Bitte sinnvoll begründen oder direkt auf Radiant verlinken. --Fritzbruno (Diskussion) 12:59, 8. Apr. 2017 (CEST)

Weil "Bogenmaß" kein Synonym zu "Radiant" ist, sondern nur in dem Artikel mitbehandelt wird. Es könnte aber prinzipiell auch ein eigener Artikel dazu existieren und vielleicht einmal entstehen. Dann wäre der Link auf "Radiant" schlecht gezielt. --Digamma (Diskussion) 19:41, 8. Apr. 2017 (CEST)

Definition am Einheitskreis

Hallo,

bin kein Mathematiker. Beschriftungen des Schaubildes rechts stimmen nicht mit dem Text überein.

Z. B. "Dieser entspricht der Strecke von ( 1 , 0 ) bis ( 1 , T ) in der Zeichnung rechts." Das ist für mich unverständlich, da ich den Punkt T in der Zeichnung rechts nicht angezeigt bekomme.

Freundliche Grüße (nicht signierter Beitrag von 2003:6a:685f:3100:a8f5:7e16:2d2a:b526 (Diskussion) 11:00, 12. Nov. 2017 (CET))

Die Zeichnung ist wohl nicht mehr im Artikel. Ich habe den Satz jetzt einfach entfernt. Danke für den Hinweis und Grüße -- HilberTraum (d, m) 14:05, 12. Nov. 2017 (CET)

Animierte Grafik zur Sinusreihe

Dieser Diskussionsbeitrag bezieht sich auf den Abschnitt "Reihenentwicklung in der Analysis" (am 9. Januar 2018) und dort auf die animierte Grafik, die zeigt, wie die Partialsummen der Taylorreihe die Sinusfunktion immer besser approximieren, wenn die Zahl der Reihenglieder erhöht wird.

Anmerkung 1:

In der Bildunterschrift wird eine Partialsumme angegeben, die bis k=2 läuft. Für k=2 muss das letzte Summenglied allerdings lauten: +x^5/(5!). In der Bildunterschrift wurde auf der rechten Seite der Gleichung bereits nach k=1 abgebrochen.

Anmerkung 2:

Im animierten Diagramm wird der Wert von N durchgehend um Eins zu groß angegeben. Das kann man wie folgt einsehen: 1.Wenn die Partialsumme der Taylorreihe des Sinus für Indices k von 0 bis 0 gebildet wird, ist der einzige Summand (-1)^0*x^0/(0!) = x. Der Graph dieser Funktion wird im animierten Diagramm allerdings mit dem Wert N=1 angezeigt.

2. Wenn die Partialsumme für Indices von 0 bis 2 gebildet wird, erhalten wir 3 Summanden. Der letzte Summand ist + x^5/(5 !). Da dies die höchste Potenz in x ist und dieser Summand ein positives Vorzeichen hat, strebt diese Partialsumme für großes x gegen unendlich. Das Diagramm zeigt für N=2 den Graph einer Partialsumme, die für großes x gegen -Unendlich strebt.

Fehlerdiagnose:

Die vermutliche Ursache des Fehlers ist, dass die Bedeutung des Summenzeichens nach den Regeln der Programmiersprache Python interpretiert wurde - in Python wird in range(1, 5) der Schlusswert 5 nicht mitgenommen. Endliche symbolische Summen sind allerdings so zu lesen, dass der Summand auch für den oberen Summationsindex ausgewertet wird.

Abschliessende Anmerkung: Das nicht animierte Diagramm, das die Approximation des Cosinus durch Taylorpolynome zeigt, ist einschliesslich seiner Bildunterschrift korrekt.

Der folgende Mathematica-Code, der z.B. auf dem Raspberry Pi unter Raspbian ausführbar ist, implementiert eine ähnliche animierte Grafik:

Approximation[x_, n_] := Module[{summe, arg, factor},
 summe = x;
 arg = x;
 factor = 1.0;
 For[i = 1, i <= n, i++,
  factor += 1;
  arg = arg*x/factor;
  factor += 1;
  arg = -arg*x/factor;
  summe += arg];
 summe]
 
 Manipulate[
     Plot[{Sin[x], Approximation[x, N]}, {x, -4*Pi, 4*Pi}, 
          PlotRange -> {{-4*Pi, 4*Pi}, {-12.0, 12}},
          AspectRatio -> 1], 
     {{N, 0, "N"}, 0, 15, 1, Appearance -> "Labeled"}]

--62.216.203.151 16:52, 9. Jan. 2018 (CET)