„Riemannsche Zahlenkugel“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
Komplexer projektiver Raum verlinkt, Großschreibung und Koordinaten in Formeln. |
Artikelausbau, manche DInge etwas (allgemein)verständlicher erläutert. Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 2: | Zeile 2: | ||
[[Datei:Riemann sphere1.svg|mini|[[Stereographische Projektion|stereographische Rückprojektionen]] der [[Komplexe Zahl|komplexen Zahlen]] <math>A</math> und <math>B</math> auf die Punkte <math>\alpha</math> und <math>\beta</math> der '''riemannschen Zahlenkugel''']] |
[[Datei:Riemann sphere1.svg|mini|[[Stereographische Projektion|stereographische Rückprojektionen]] der [[Komplexe Zahl|komplexen Zahlen]] <math>A</math> und <math>B</math> auf die Punkte <math>\alpha</math> und <math>\beta</math> der '''riemannschen Zahlenkugel''']] |
||
In der [[Mathematik]] ist die '''Riemannsche Zahlenkugel''' <math>\hat{\Complex}= \mathbb{C}\cup\{ \infty\} </math> die [[Riemannsche Fläche]], die sich aus der Hinzunahme eines ''Punktes in der Unendlichkeit'' zu der [[Komplexe Zahlenebene|komplexen Ebene]] ergibt. Sie ist der erste nichttriviale [[Komplexer projektiver Raum|komplexe projektive Raum]] und geht zurück auf [[Bernhard Riemann]]. |
In der [[Mathematik]] ist die '''Riemannsche Zahlenkugel''' <math>\hat{\Complex}= \mathbb{C}\cup\{ \infty\} </math> die [[Riemannsche Fläche]], die sich aus der Hinzunahme eines ''Punktes in der Unendlichkeit'' zu der [[Komplexe Zahlenebene|komplexen Ebene]] ergibt. Anschaulich gesehen wird die Ebene der komplexen Zahlen an einem Punkt zu einer Kugel zusammengeklebt. Sie ist der erste nichttriviale [[Komplexer projektiver Raum|komplexe projektive Raum]] und geht zurück auf [[Bernhard Riemann]]. |
||
== Topologie und komplexe Struktur == |
|||
Weiter wird auf der Riemannschen Zahlenkugel wie folgt eine [[Topologie (Mathematik)|Topologie]] definiert: [[Offene Menge]]n sind einerseits die offenen Mengen in <math> \mathbb{C}</math> und andererseits die bezüglich <math> \mathbb{C}\cup\{ \infty\} </math> gebildeten Komplemente von [[Kompakte Menge|kompakten Teilmengen]] von <math> \mathbb{C}</math>. Der so definierte [[topologischer Raum|topologische Raum]] stellt eine [[Kompaktifizierung]] der komplexen Ebene dar. [[Topologie (Mathematik)|Topologisch]] ist sie äquivalent zur Einheitssphäre <math>S^2</math>. Mit der [[Chordale Metrik|chordalen Metrik]] wird die Zahlenkugel zu einem [[Metrischer Raum|metrischen Raum]]. Diese Metrik induziert die gleiche Topologie, die durch die [[Einpunktkompaktifizierung]] auf die Zahlenkugel induziert wird. |
|||
Die Topologie auf <math>\hat{\C}</math> wird folgendermaßen erzeugt: Man bezeichnet mit <math>P: S^2\to \hat{\C}</math> die stereographische Projektion durch den Nordpol und bildet zusätzlich <math>\infty</math> auf den Nordpol ab, d.h. |
|||
:<math>P(x_1,x_2,x_3) = \begin{cases} |
|||
\frac{x_1}{1-x_3} + \mathrm{i} \frac{x_2}{1-x_3} & x \neq (0,0,1), \\ |
|||
\infty & x = (0,0,1). |
|||
\end{cases}</math> |
|||
<math> P </math> ist invertierbar, da die stereographische Projektion invertierbar ist und man <math>P^{-1}(\infty) = (0,0,1)</math> hat. Die Funktion <math>\chi: \hat{\mathbb{C}}^2 \to \mathbb{R}</math>, gegeben durch |
|||
<math> \chi(x,y) = \lVert P^{-1}(x) - P^{-1}(y) \rVert_2, </math> |
|||
definiert eine Metrik auf <math>\hat{\C}</math> und heißt [[chordale Metrik]]. Durch die von der Metrik erzeugten Topologie sind <math>P</math> und <math>P^{-1}</math> stetig. Daher ist <math>\hat{\C}</math> homöomorph zu <math>S^2</math>, woher die Bezeichnung Zahlenkugel rührt. |
|||
| ⚫ | Die [[komplexe Struktur]] der Riemannschen Zahlenkugel wird durch zwei [[Atlas (Mathematik)#Karte|Karten]] gegeben. Die erste ist auf <math>\mathbb C</math> definiert und ist die Identität. Die zweite ist auf der [[Umgebung (Mathematik)|Umgebung]] <math>[\mathbb C \cup \{\infty\}] \setminus \{0\}</math> des unendlich fernen Punkts definiert durch |
||
| ⚫ | Die komplexe Struktur der Riemannschen Zahlenkugel wird durch zwei [[Atlas (Mathematik)#Karte|Karten]] gegeben. Die erste ist auf <math>\mathbb C</math> definiert und ist die Identität. Die zweite ist auf der [[Umgebung (Mathematik)|Umgebung]] <math>[\mathbb C \cup \{\infty\}] \setminus \{0\}</math> des unendlich fernen Punkts definiert durch |
||
:<math>z \mapsto |
:<math>z \mapsto |
||
\begin{cases} \frac 1z, & \text{falls } z \in \mathbb C,\\ |
\begin{cases} \frac 1z, & \text{falls } z \in \mathbb C,\\ |
||
| Zeile 12: | Zeile 26: | ||
\end{cases}</math> |
\end{cases}</math> |
||
== Rechenregeln == |
|||
Anschaulich handelt es sich um eine Kugel vom Radius 1, deren Nordpol auf <math>(0,0,1)</math> liegt (man darf die Kugel beliebig wählen, solange ihr Nordpol <math>(0,0,1)</math> ist). Dem unendlich fernen Punkt <math>\infty</math> wird dieser Nordpol <math>U</math> der Kugel zugeordnet und jedem Punkt <math>P</math> der komplexen Zahlenebene der von <math>U</math> verschiedene Schnittpunkt der Kugeloberfläche mit der Geraden durch <math>PU</math> ([[stereografische Projektion]]). |
|||
Auf der Riemannschen Zahlenkugel wendet man im wesentlichen dieselben Rechenregeln wie auf den komplexen Zahlen an. Daneben gelten noch folgende Regeln:<ref>{{MathWorld|title=Directed Infinity|id=DirectedInfinity}}</ref> So ist z. B. zwar der Grenzwert von <math>1/x</math>, wobei <math>x</math> eine positive reelle Zahl ist, die gegen <math>0</math> geht, eine gerichtete Unendlichkeit mit dem komplexen Argument <math>0</math> Für alle [[Komplexe Zahl|komplexen]] <math>z, w \ne 0</math> und alle [[Reelle Zahl|reellen]] <math>x \ne 0</math> gilt: |
|||
| ⚫ | |||
* <math>z \cdot \infty = \arg(z) \cdot \infty</math> |
|||
* <math>0 \cdot \infty</math> bleibt undefiniert, ebenso <math> \frac{z \ \infty}{w \ \infty}</math> |
|||
* <math>x \cdot z \cdot \infty = \sgn(x) \cdot \arg(z) \cdot \infty</math> |
|||
* <math>(w \cdot \infty) \cdot (z \cdot \infty) = \arg(w \cdot z) \cdot \infty</math> |
|||
Hier ist <math>\arg</math> die durch <math>\arg(z) := \frac{z}{\left|z\right|}</math> für alle komplexen Zahlen <math>z \ne 0</math> erklärte [[Argumentfunktion]] und <math>\sgn</math> ist die für alle reellen Zahlen definierte [[Vorzeichenfunktion]]. |
|||
== Eigenschaften und Anwendungen == |
|||
* Topologisch ist diese geschlossene Riemannsche Fläche vom [[Geschlecht (Fläche)|Geschlecht]] <math> 0 </math> bis auf [[Homöomorphie]] eindeutig, das gilt aber nicht für [[Biholomorphie]], d.h. es ließe sich noch eine andere komplexe Struktur finden. |
|||
* Auf Basis des [[Satz von Riemann-Roch|Satzes von Riemann-Roch]] kann man zeigen, dass jede kompakte Riemannsche Fläche eine Einbettung in einen projektiven Raum besitzt. Des Weiteren lässt sich dann zeigen, dass jede Riemannsche Fläche biholomorph zu einer [[Projektive Varietät|projektiven Varietät]] der Dimension <math>1</math> ist, d.h. Riemannsche Flächen lassen sich als Nullstellenmenge von homogenen Polynomen darstellen.<ref>Jürgen Jost: ''Compact Riemann Surfaces. An Introduction to Contemporary Mathematics''. 2. Auflage, Springer Berlin Heidelberg, 2002, S. 234 ff.</ref> |
|||
| ⚫ | |||
* Eine [[meromorphe Funktion]] kann man als eine [[holomorphe Funktion]] in die Riemannsche Zahlenkugel interpretieren. |
|||
* Die [[verzweigte Überlagerung|verzweigten Überlagerungen]] über der Riemannschen Zahlenkugel führen zur Theorie der [[Hurwitz-Zahl|Hurwitz-Zahlen]]. |
|||
== Siehe auch == |
== Siehe auch == |
||
* [[Projektiver Raum]] |
* [[Projektiver Raum]] |
||
== Literatur == |
|||
* Otto Forster: ''Riemannsche Flächen'', Springer Berlin Heidelberg, 1977. |
|||
* Klaus Lamotke: ''Riemannsche Flächen'', Springer-Verlag Berlin Heidelberg, 2009. |
|||
== Weblinks == |
== Weblinks == |
||
* [https://www.thphys.uni-heidelberg.de/~hefft/vk1/#816b1d Erklärung von Klaus Hefft (Institut für Theoretische Physik, Uni-Heidelberg)] |
* [https://www.thphys.uni-heidelberg.de/~hefft/vk1/#816b1d Erklärung von Klaus Hefft (Institut für Theoretische Physik, Uni-Heidelberg)] |
||
== Einzelnachweise == |
|||
<references/> |
|||
[[Kategorie:Funktionentheorie]] |
[[Kategorie:Funktionentheorie]] |
||
Version vom 12. Mai 2024, 16:48 Uhr
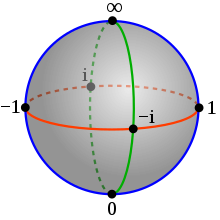

In der Mathematik ist die Riemannsche Zahlenkugel die Riemannsche Fläche, die sich aus der Hinzunahme eines Punktes in der Unendlichkeit zu der komplexen Ebene ergibt. Anschaulich gesehen wird die Ebene der komplexen Zahlen an einem Punkt zu einer Kugel zusammengeklebt. Sie ist der erste nichttriviale komplexe projektive Raum und geht zurück auf Bernhard Riemann.
Topologie und komplexe Struktur
Die Topologie auf wird folgendermaßen erzeugt: Man bezeichnet mit die stereographische Projektion durch den Nordpol und bildet zusätzlich auf den Nordpol ab, d.h.
ist invertierbar, da die stereographische Projektion invertierbar ist und man hat. Die Funktion , gegeben durch
definiert eine Metrik auf und heißt chordale Metrik. Durch die von der Metrik erzeugten Topologie sind und stetig. Daher ist homöomorph zu , woher die Bezeichnung Zahlenkugel rührt.
Die komplexe Struktur der Riemannschen Zahlenkugel wird durch zwei Karten gegeben. Die erste ist auf definiert und ist die Identität. Die zweite ist auf der Umgebung des unendlich fernen Punkts definiert durch
Rechenregeln
Auf der Riemannschen Zahlenkugel wendet man im wesentlichen dieselben Rechenregeln wie auf den komplexen Zahlen an. Daneben gelten noch folgende Regeln:[1] So ist z. B. zwar der Grenzwert von , wobei eine positive reelle Zahl ist, die gegen geht, eine gerichtete Unendlichkeit mit dem komplexen Argument Für alle komplexen und alle reellen gilt:
- bleibt undefiniert, ebenso
Hier ist die durch für alle komplexen Zahlen erklärte Argumentfunktion und ist die für alle reellen Zahlen definierte Vorzeichenfunktion.
Eigenschaften und Anwendungen
- Topologisch ist diese geschlossene Riemannsche Fläche vom Geschlecht bis auf Homöomorphie eindeutig, das gilt aber nicht für Biholomorphie, d.h. es ließe sich noch eine andere komplexe Struktur finden.
- Auf Basis des Satzes von Riemann-Roch kann man zeigen, dass jede kompakte Riemannsche Fläche eine Einbettung in einen projektiven Raum besitzt. Des Weiteren lässt sich dann zeigen, dass jede Riemannsche Fläche biholomorph zu einer projektiven Varietät der Dimension ist, d.h. Riemannsche Flächen lassen sich als Nullstellenmenge von homogenen Polynomen darstellen.[2]
- Die Automorphismen, also die biholomorphen Abbildungen der riemannschen Zahlenkugel auf sich selbst, bilden die Gruppe der Möbiustransformationen.[3]
- Eine meromorphe Funktion kann man als eine holomorphe Funktion in die Riemannsche Zahlenkugel interpretieren.
- Die verzweigten Überlagerungen über der Riemannschen Zahlenkugel führen zur Theorie der Hurwitz-Zahlen.
Siehe auch
Literatur
- Otto Forster: Riemannsche Flächen, Springer Berlin Heidelberg, 1977.
- Klaus Lamotke: Riemannsche Flächen, Springer-Verlag Berlin Heidelberg, 2009.
Weblinks
Einzelnachweise
- ↑ Eric W. Weisstein: Directed Infinity. In: MathWorld (englisch).
- ↑ Jürgen Jost: Compact Riemann Surfaces. An Introduction to Contemporary Mathematics. 2. Auflage, Springer Berlin Heidelberg, 2002, S. 234 ff.
- ↑ Forster, S. 120
















![{\displaystyle [\mathbb {C} \cup \{\infty \}]\setminus \{0\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66d2b873ca47c1d7cc7195e9aa8a05f35de1e297)















